Mesure de la Terre !

Que la Terre est belle vue de l'espace, non ?
Quelle chance nous avons tous de vivre au XXIème siècle et de pouvoir comtempler notre planète !
Mais, qu'elle semble petite vue de là-haut...
En tout cas, c'est bien la preuve qu'elle est ronde...et qu'Atlas n'existe pas.
Que de chemin parcouru pour en arriver là !
Parmi les défis de haute couture, mesurer le tour de taille de la Terre en est un... de taille !

Sciensass est fier de vous présenter Vassensouaff, son envoyé spécial, éminent connaisseur des longues distances, dont la présentation n'est plus à faire tant sa renommée est maintenant internationale ! Il relate dans nos colonnes, en exclusivité pour nous, l'épopée de la mesure de la Terre, depuis la nuit des temps (du moins ce que l'on en connaît !) à aujourd'hui..
Avant d'admirer la Terre depuis l'espace, il faudrait peut être d'abord redescendre sur Terre et commencer par le commencement.
Plate ou ronde ?
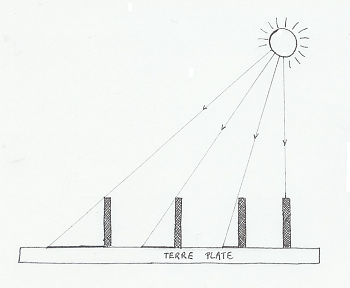
La terre est complètement plate, comment pourrait-il en être autrement ?
Quand je regarde autour de moi, à mon échelle de petit dromadaire, j'ai carrément l'impression que la terre est plate, hormis bien sûr quelques reliefs, dunes, montagnes et autres vallées, mais globalement... plate !
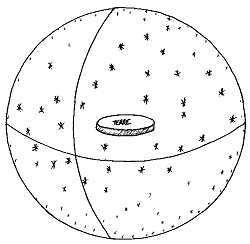
Et les hommes s'y sont laissés tromper aussi d'ailleurs ! Donc, au VIème avant JC, pour les hommes, la Terre est plate comme une assiette et elle est entourée par la voute céleste, sphère sur laquelle reposent tous ces petits points brillants que nous savons aujourd'hui être des étoiles. La sphère de la voute céleste représente la perfection du domaine des dieux, la sphère étant la forme la plus parfaite qui soit et il n'y a rien de plus parfait que les dieux il va sans dire. Bien sûr, personne "n'habite" sous la Terre !
Comment pourait-on vivre la tête en bas ?
Si la voute céleste, habitat des dieux, est par définition inaccessible, l'exploration de la "galette" terrestre est permise puisqu'elle est le domaine des humains, monde imparfaitement plat et chacun sait très bien que la perfection n'existe pas dans ce bas monde... En 1840, les historiens allemands ont reconstitué la carte du monde vu par Anaximandre (610-546 av JC).

A cette époque le monde est méditerranéen ! Globe allemand plat, quoi... Cette carte est assez fidèle à la méditerranée que nous connaissons aujourd'hui, c'est dire l'habileté des explorateurs de l'époque ! Par contre, au-delà de la méditerranée... c'est le flou artistique : la Terre est entourée par le "fleuve océan" dont nul ne connaît les limites, ni si l'eau coule au-delà des bords de l'assiette. Mais il faut tout de même bien que l'eau de pluie s'échappe quelque part, non ? En l'état, une Terre plate à bords indéfinis est tout simplement immesurable : comment mesurer le diamètre d'une assiette si on ne sait même pas où en sont les bords ! On peut comprendre par ailleurs que les hommes aient eu peur de voir disparaître un jour le soleil, boule de feu bienfaisante sans laquelle le noir de la nuit fait si froid dans le dos, avec tous les prédateurs qui rôdent...Oui, oui, d'accord, c'était à une époque encore plus lointaine, mais tout de même, ce soleil a-t-il une raison particulière d'apparaître d'un bord de l'assiette, de disparaître de l'autre bord, de passer sous l'assiette et de recommencer ce qu'on a appelé le lendemain, sans jamais s'arrêter ? Je crois que moi aussi, j'aurais inventé un dieu capable de cette prouesse et je l'aurais sans doute imploré de continuer de nous apporter sa chaleur et sa lumière sans nous abandonner...Mais, aujourd'hui, on pourrait s'en passer non ? Les babyloniens imaginaient même, il y a plus de 5000 ans, un tunnel sous le monde pour laisser passer le Soleil ! Mais cette vision du monde va radicalement changer et en très peu de temps.

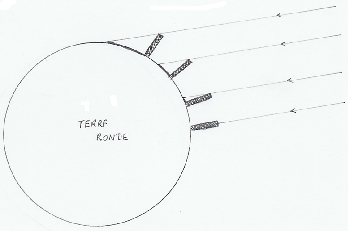
En effet, de nombreuses observations semblent bizarres et en contradiction avec le modèle d'une terre plate. Je vous en cite quelques exemples.
La lune et le soleil sont ronds
La première et la plus évidente est que la Lune et le Soleil sont ronds, du moins ils le semblent, alors pourquoi pas la Terre ? S'ils ne sont pas ronds (sphériques) mais tous deux plats comme une pièce de monnaie, alors ils se présentent à nous de face (ou de pile c'est au choix...), et toujours de face ce qui serait une belle coïncidence ! Mais après tout pourquoi pas ? Nous savons justement que la Lune nous présente toujours la même face ! Disons alors simplement que cet exemple met la puce à l'oreille. De parler de puce, voilà déjà que ça me démange.
La vigie
Quand un bateau s'éloigne du port, les personnes restées à terre voient disparaître la coque du navire avant les voiles ou encore la Terre est toujours aperçue par la vigie en haut du mât avant les marins restés sur le pont, sinon à quoi servirait une vigie ?
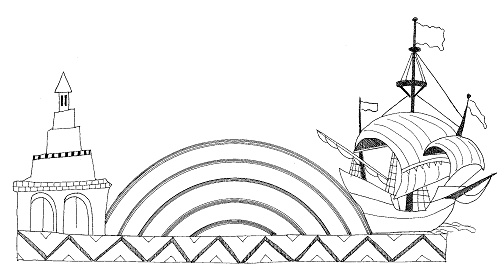
La mer semble donc bossue. Cette Terre plate assortie d'une mer bossue pourrait nous faire sourire aujourd'hui, mais attention, les hommes de cette époque étaient exactement les mêmes qu'aujourd'hui, largement aussi intelligents ! D'ailleurs, les Ioniens vivaient déjà dans une société où le pouvoir appartenait à l'assemblée des citoyens : une sorte de démocratie ; les discussions y étaient publiques et tout le monde pouvait y participer. Nous n'avons pas fait mieux depuis ! Jaurais même l'impression que ça se dégrade !! Et n'oublions pas que ce que nous faisons aujourd'hui prêtera sans doute à sourire dans quelques siècles ; avons-nous tort pour autant ? Si tu penses que oui, cher lecteur, alors la science compte sur toi pour nous le prouver !
Les phases de la Lune
PQ, PL, DQ et NL comme on peut le lire sur les calendriers, pour premier quartier, pleine Lune etc... Si la Lune était plate comme une pièce de monnaie nous faisant toujours face, on la verrait toujours soit comme un disque lumineux, quand la Terre se trouve entre le Soleil et la Lune, soit on ne la verrait pas du tout, quand c'est la Lune qui se trouve entre la Terre et le Soleil, on serait alors ébloui par le Soleil. Mais alors, pas de quartiers ! On ne peut expliquer les phases de la Lune que si elle est sphérique ! Les schémas suivants sont suffisamment explicites ! Du moins, je l'espère !
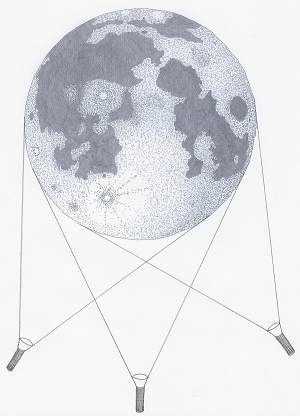

A gauche, elle apparaît toujours ronde quelque soit sa position par rapport au soleil (représenté ici par la lampe). La lune est plate comme une pièce de monnaie et nous fait face. Alors que le schéma de droite montre une phase avec la lune sphérique. Cette configuration est très facile à reproduire sur Terre en utilisant la lumière d'une bougie qui éclaire une orange par exemple. Etant donné qu'on observe des phases de Lune, elle est certainement sphérique, alors pourquoi pas la Terre ?
Les éclipses de Lune
Lors des éclipses de Lune, la terre projette sur la Lune une ombre arrondie, elle est donc sans doute sphérique. Voilà ce qu'on peut observer lors d'une éclipse :

On ne peut pas confondre cette image avec une phase de la Lune, d'abord parce que le cycle des phases de Lune a une période d'environ 28 jours quand l'éclipse de Lune ne dure que quelques heures, d'autre part l'éclipse de Lune n'a lieu qu'à la pleine Lune et l'ombre projetée par la Terre "croque", au début et à la fin de l'éclipse, un tout petit morceau de la Lune, ce qu'on n'observe jamais lors des phases parce que l'ombre passe toujours par deux points diamètralement opposés. (voir schéma de phase ci-dessus)
La hauteur de l'étoile polaire
La hauteur de l'étoile polaire au dessus de l'horizon n'est pas la même en Grèce et en Egypte ! Je sais, c'est stupéfiant ! La Terre tourne sur elle-même autour d'un axe de rotation qui passe par ses pôles. Lors de sa rotation, les étoiles dans le ciel bougent toutes de concert : elles décrivent des arcs de cercles. L'étoile polaire a la particularité de se touver sur l'axe de rotation de la Terre et semble donc immobile dans le ciel contrairement à toutes les autres ; tout cela, c'est bien sûr ce que nous savons aujourd'hui (avec une Terre sphérique), mais à l'époque...
Si la Terre est plate, une étoile immobile et très lointaine dans le ciel devrait être vue à la même hauteur par rapport à l'horizon et ce quelque soit le lieu d'observation à la surface de la Terre, ce qui n'est pas le cas en réalité. Comment l'expliquer ?
En naviguant vers l'ouest !
Le pharaon phénicien Néchao avait envoyé des marins faire le tour de l'Afrique. A leur retour, ils racontèrent que pendant leur voyage et alors qu'ils naviguaient vers l'ouest, le Soleil paraissait à tribord (la droite du navire) alors qu'on l'avait toujours vu à bâbord ! Bien sûr, cela n'est pas possible sur une Terre plate : on a donc ignoré ces récits de matelots ignorants ou sans doute complètement ivres. Cela est impossible sur une Terre plate, mais qu'en est-il si la Terre est sphérique ? Cher lecteur, imagine que tu sois le Soleil (inutile de te prendre pour une lumière non plus...)

Les deux navires de gauche, se dirigeant vers l'ouest, te verraient à bâbord pour celui de l'hémisphère nord et à tribord pour l'autre ce qui est impossible sur une Terre plate : tous les bateaux se déplaçant vers l'ouest te verraient à babord ! Le plus difficile à comprendre dans tout ça : comment peut-on marcher la tête en bas de l'autre côté de la Terre si celle-ci est ronde ? De là est d'ailleurs né le mot antipode : pieds contre pieds (anti : contre et pode venant du latin pedis qui signifie pied). Il y a sans doute assez d'arguments pour penser que la Terre est sphérique, non ? Et c’est d'ailleurs la même chose pour notre ombre. Dans l’hémisphère nord, notre ombre est toujours orientée… du côté nord alors que c’est le contraire dans l’hémisphère sud ! Pour trouver le sud, les européens regardent le Soleil à midi, en Afrique du sud, le soleil de midi est au… nord ! Réaliser une maison solaire avec les panneaux solaires plein nord, quelle aberration !! Le soleil se lève à l’est et se couche à l’ouest, Sciensass ne nous apprend rien en disant cela et c'est toujours vrai, dans l'hémisphère nord comme dans le sud, et pourtant…

La course du soleil dans le ciel se fait dans le sens des aiguilles d’une montre dans l’hémisphère nord (quand on regarde le soleil bien sûr) et dans l’autre sens dans l’hémisphère sud ! Ah ! Un petit voyage dans l'hémisphère sud, rien que pour voir le Soleil se lever sur ma droite et se coucher sur ma gauche quand je le regarde ! Pourquoi pas le Brésil ? Bon,cessons de rêver ! Chaque fois que notre instituteur organisait une course d’orientation, il y avait toujours quelques égarés qu’il fallait secourir, perdus on ne sait où. A quand une course d’orientation dans l’hémisphère sud pour des petits français ? Histoire de se compter à la fin ! Il faut bien reconnaître que les humains n'ont pas du tout le sens de l'orientation des dromadaires !
Le tour de taille !
Alors comme ça, on prétend mesurer le tour de la Terre ! Certe, elle est ronde et on peut en faire le tour, Mais, c'est tout de même mission impossible ! Je vous imagine les amis, faisant le tour de la Terre en déroulant un fil derrière vous ! Quel spectacle : je vous vois d'ici : marcher, nager ou encore voler... à travers monts et montagnes, mers et océans, déserts et forêts vierges, guerres et paix...Et vous comptez sans doute mesurer la longueur du fil une fois la boucle bouclée ! Mais, enfin, combien de tonnes de fil vous faudra-t-il donc ? Sans compter la dimension de la jolie pelote à dérouler ! Et mesurer ensuite sa longueur astronomique ne doit pas non plus être une mince affaire : Une fois le tour de la Terre effectué, il faudra couper la ficelle, et recommencer le périple dans l'autre sens en la mesurant au fur et à mesure... A moins que vous ayez pris soin de graduer le fil avant de partir !!!

Je peux vous prêter le mien, il n'est pas bien lourd.
Enfin, je voulais dire dense !
Quelqu'un connaît-il la masse linéique de mon fil ?
Oui ! Bravo ! Alors le calcul de la masse de fil nécessaire pour mesurer la Terre n'est plus qu'un jeu d'enfant !
(Merci de contacter Sciensass pour donner la réponse)
Le fil d'araignée est des plus résistants, plus costaud que l'acier, certe, mais un peu collant, je ne sais pas si cela sera très pratique pour dérouler la petite pelote, enfin bref...
Et, en combien de temps pensez-vous faire le tour de la Terre ?
Enfin, je sais bien qu'au XXIème siècle, plus rien ne nous étonne, qu'avec les progrès de la technique et sans doute un laser ou autre photon, mesurer la Terre n'est qu'une formalité.
Alors, on va nous le dire à la fin : qui, quand, comment ?
Et, que viennent faire des dromadaires dans ces pages d'abord ?
Nous donner la réponse, pardi ! Ils la connaissent depuis si longtemps !

Et pour cause, c'est nous qui l'avons mesurée, et à pinces, s'il vous plaît ! Bon, en fait, les dromadaires ont un peu aidé Eratosthène et c'est à lui seul que revient la paternité de cette mesure ! Mais attention ! Quasiment sans bouger de chez lui ! J'allais dire le cul dans son fauteuil, mais je n'ose pas : disons qu'à coté de tous les stades que nous avalons par jour, Eratosthène peut passer pour un aï (je veux dire paresseux bien sûr, vous n'auriez tout de même pas confondu avec haï ?) Et qui plus est, pas au XXIème siècle, non, mais bien avant JC, vers 275 av JC pour être un peu plus précis. Et vous pensez bien qu'à cette époque, la technologie n'était pas ce qu'elle est aujourd'hui, on ne parlait pas encore au téléphone ! On ne connaissait pas le chat non plus !

On m'appelle ? Mais non, on a dit chat, pas chat ! Alors, comment s'y est-il pris pour mesurer le tour de la Terre ? En mesurant l'ombre d'un piquet, si si je vous assure ! Alors, pour ceux qui ne sont pas encore au courant, voilà l'histoire : Vous n'êtes pas sans avoir déjà remarqué que les rayons du Soleil qui nous arrivent à la surface de la Terre sont localement parallèles entre eux. Quand je dis localement, j'entends une petite portion de désert comme celle qu'on peut visiter dans une journée ou tout simplement la taille d'une ville. Cela n'avait pas échappé non plus à Eratosthène. Observation qu'il a aussitôt mise à profit. Pourtant... l'ombre des objets n'est pas la même selon l'endroit où on se trouve à la surface de la Terre. A Alexandrie, (je vous laisse chercher où cela se trouve !) Erastosthène dirigeait la bibliothèque, ce qui représentait une très haute fonction à l'époque. Comme Alexandrie était une ville de très grande renommée culturelle et commerciale, Eratosthène entendit un jour parler d'un puits aux propriétés remarquables, situé à Syène (Assouan actuel) plus au sud d’Alexandrie. Chaque année, le 21 juin, jour du solstice d'été, le Soleil éclaire directement le fond du puits. Ce jour là, les rayons du Soleil sont donc verticaux à Syène, mais pas à Alexandrie !!! Quand je disais que l'ombre n'est pas la même partout ! Alors là, de deux choses l'une :
Soit la Terre est plate et le Soleil en est tout près, ou la Terre est sphérique et le Soleil en est très loin ! Comment trancher entre ces deux possibilités ? A l'époque de mes aïeux, comtemporains d'Eratosthène, il y avait déjà bien longtemps qu'on observait le monde et qu'on tentait de le comprendre. Aussi, tous les faits énoncés plus hauts, en faveur d'une Terre ronde, étaient déjà bien connus. Donc Eratosthène a choisi : pour lui, la Terre est ronde ! Le Soleil ne peut pas être très près : on savait déjà qu'entre la Terre et la Lune, on pouvait "mettre" plus de 100 fois la Lune et le Soleil est forcément encore plus loin, puisque lors d'une éclipse de Soleil, la Lune passe entre la Terre et le Soleil.
Une histoire d'angles
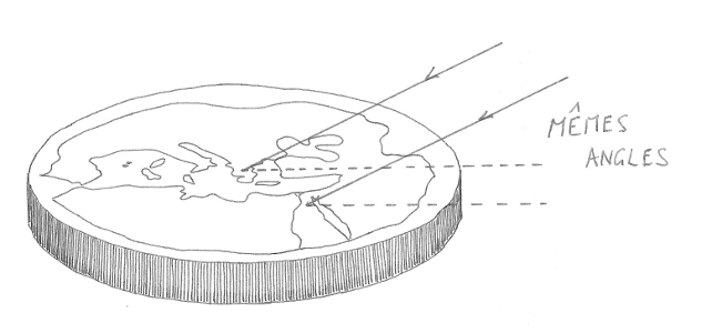
Alors récapitulons : les rayons du Soleil arrivent verticalement à Syène le 21 juin, mais pas à Alexandrie. Pourtant, le Soleil étant très loin, ses rayons lumineux arrivent jusqu'à la Terre parallèles entre eux, la situation est la suivante :
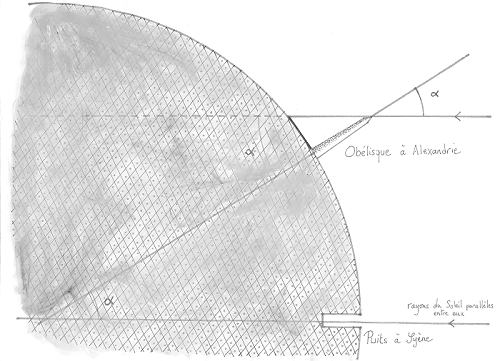
Voilà notre homme parti à l’assaut de la Terre ! Etatosthène trouva là le moyen d’en mesurer le rayon. Et d'une simplicité ! Il suffisait de mesurer la longueur de l’ombre de l’obélisque et sa hauteur ! Et c'est tout ! A la portée de n'importe quel enfant de l'école primaire ! Alors, bien sûr, il suffisait, il suffisait... Facile à dire : c'est toujours après coup qu'on se dit : mais pourquoi n'y ai-je pas pensé plus tôt ? n'est-ce pas ? Serais-je sot ? Mais non, c'est simplement que quelqu'un l'avait déjà fait avant moi ! Te voilà rassuré ? Alors disons qu'il suffisait...d'y penser ! En effet, les angles $\alpha$ repérés sur le schéma ci-dessus sont tous égaux. Tous ceux qui ont fait un petit tour par le collège le savent bien. On les appelle des angles opposés au sommet et angles alterne interne. Cela me rapelle même le théorème de... Thalès. Eratosthène mesura donc cet angle le 21 juin avec l'ombre de l'obélisque. L'histoire ne dit pas à quel point l'impatience de notre héros devait être à son comble en attendant ce jour exceptionnel ! Mais nous l'imaginons facilement ! Partageons donc un peu son exaltation !
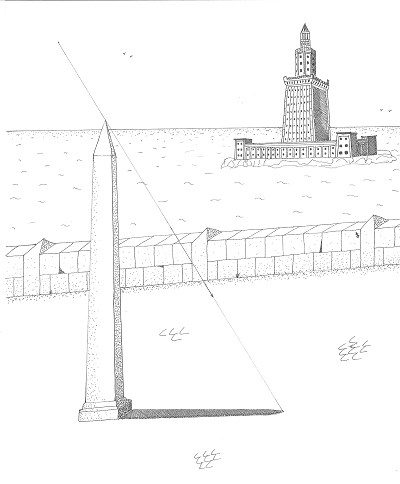
En mesurant L la longueur de l'ombre de l'obélisque et H sa hauteur, on peut calculer l'angle $\alpha$ avec un tantinet de trigonométrie : Tous les dromadaires savent faire cela !
Il trouva alors 7,2 degrés.
Le plus difficile alors, était de mesurer la distance (dAS) entre Alexandrie et Syène, assez près l'une de l'autre pour espèrer réussir, mais assez éloignées pour ne pas pouvoir utiliser une corde ou la triangulation... Tu ne connaîs pas la triangulation ? Ne t'inquiète pas, nous en reparlons un peu plus loin. Si on connaît cette distance pour un angle $\alpha$, on pourra trouver la circonférence de la Terre et donc son tour de taille ! Et c'est là que nous les dromadaires sauvâmes Eratosthène !! Eh oui ! il fallait bien quelqu’un pour mesurer la distance de Syène à Alexandrie ! C'est en comptant le nombre de jours nécessaires pour aller de Syène à Alexandrie à dos de dromadaire (halte à l'exploitation) et en estimant la distance moyenne parcourue par jour par un dromadaire moyen qu' Eratosthène trouva 5000 stades. Vous vous rendez compte ! 5000 stades ! J'en vouvoie tellement je suis impressionné !
Bravo Eratosthène !

C'est ce qui s'appelle une jolie balade de santé et sans boire une seule goutte d'eau, s'il vous plaît ! Donc récapitulons : 5000 stades pour un angle de 7,2° ; sachant qu'un tour complet représente 360° quelle est la circonférence de la Terre ? J'espère que vous savez faire le calcul parce que c'est quand même Eratosthène qui a fait le plus dur ! 250000 stades, bravo ! Bien sûr, il suffisait de remarquer que 360° équivalent à 50 fois les 7,2° mesurés par Eratosthène et donc que le périmètre de la Terre vaut lui aussi 50 fois la distance entre Syène et alexandrie. Une simple règle de trois, si je comprends bien ! Le seul petit problème, c'est qu'on ne sait pas du tout quel stade notre homme a utilisé : il y en avait en effet plusieurs en usage à cette époque. Inutile de se moquer, moi, j'en connais qui utilisent encore des pouces, pieds et autres miles, alors... Si c'est le stade égyptien, de 157,5 de nos mètres actuels, alors la précision est vraiment remarquable : on trouve 39400 km.
Chapeau bas, messieurs les dromadaires.
Pas bientôt fini d'se prendre pour le roi du désert celui-ci ? Et voilà ! Eratosthène a réalisé un exploit ! Il fallait tout de même le faire ! Nous nous rendons finalement compte que notre planète Terre, qui nous semble si grande quand on essaie de la visiter, est finalement plutôt petite et bien fragile ! Deux, trois millénaires après Eratosthène, l'homme s'imagine avoir domestiquer la nature, mais il suffit qu'il neige en hiver pour que les voitures ou les trains ne roulent plus, ou qu'un petit volcan se réveille pour que plus aucun avion ne puisse voler et voilà notre petit humain remis à sa place : celle qui lui revient ! Et, malgré tout le génie que je suis forcé de te reconnaître, petit homme, aussi bien dans les sciences, que dans l'architecture, les arts, la poésie et j'en passe, il serait bon de rester modeste et de ne pas oublier que la Terre est notre mère à tous et qu'elle t'a enfanté toi aussi. Attention de ne pas scier la branche sur laquelle... Et je ne parlerai pas de ta folie guerrière, inégalée à ce jour !

Non seulement, il se prend pour le roi du désert, mais en plus il se permet de faire la morale ! A croire qu'il veut prendre la place de l'homme ! Le calife à la place du calife ! Mais où va-t-on ?
Clair de Terre
Aujourd'hui, au XXIème siècle, nous ne mesurons pas la chance que nous avons de voir la Terre, boule flottante dans l'espace, grâce aux photographies prises par les satellites. Elle nous est même tellement familière. Nous savons très bien qu'elle n'a ni haut, ni bas, (Newton et sa théorie de la gravitatin est passée par là) qu'elle n'a pas besoin d'Atlas pour la porter (et qui portait Atlas ?) Que dire des spationautes qui ont pu La voir de visu, lors de leurs rotations autour de la Terre à bord de la station spaciale internationale ! Cette station qui réalise plusieurs tours de la Terre par jour permet aux spationautes d'observer les phases de la Terre, tantôt la face claire, tantôt la face sombre ! Quels chanceux : imaginez un peu : Rêver au clair de la Terre ! Lire un poème au clair de Terre ! Les luniens ont ce privilège, mais nous terriens profitons du clair de Lune et nous sommes finalement assez peu à en profiter dans le cosmos. L'aventure continue !
Distance Terre-Lune
La connaissance de la taille de la Terre a permis de s'échapper de notre planète et de mesurer des distances plus grandes encore et tout d'abord la distance Terre-Lune. Mais pour cela, on a besoin de la taille de la Lune.
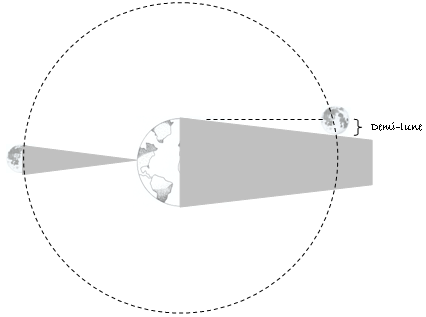
Or, on connaissait depuis longtemps déjà, la taille relative de la Lune par rapport à celle de la Terre. C'est-à-dire que le diamètre de la Lune est quatre fois plus petit que celui de la Terre. Comment le savait-on ?
Si l’on suppose que les rayons du Soleil sont parallèles entre eux, alors l’ombre de la Terre correspond à un cylindre de même diamètre que celui de la Terre.
Or, lors d’une éclipse de Lune, cette dernière passe dans l’ombre de la Terre. Il semble que nous devons cette méthode à Aristarque de Samos (310-230 av JC). Il mesure la durée qui sépare le début de l’entrée de la Lune dans la zone d’ombre (première image) et la disparition totale de la Lune (deuxième image).
Il trouve environ 50 minutes.
La Lune se déplace donc de son diamètre en 50 minutes.
Il mesure ensuite la durée nécessaire à la Lune pour traverser la totalité de la zone d’ombre qui correspond au diamètre de la Terre (image 3).
Et il trouve 200 minutes.
Si on suppose que la vitesse de la Lune reste constante pendant toute la durée de l’éclipse, elle parcourt une distance égale à son diamètre en 50 minutes et le diamètre de la Terre en quatre fois plus, soit 200 minutes.
La Terre a donc un diamètre quatre fois plus grand que celui de la Lune. La mesure du diamètre de la Terre permet alors de déduire celui de la Lune.
Sauras-tu cher lecteur le retrouver en stades ?
Et nous pouvons donc en venir à la distance Terre-Lune : depuis le temps que je promets la Lune à ma femme, je veux dire ma dromadaire, je vais enfin savoir combien de temps durera la croisière pour y aller à dos de... ah oui, à dos de quoi au fait ? La Lune n'est pas éblouissante (elle ne renvoie que 7% de la lumière qu'elle reçoit) et peut être observée sans problème à l’œil nu. Comment faire autrement d’ailleurs, on n’a jamais vu un dromadaire avec des lunettes ! On peut masquer parfaitement la Lune avec l'ongle de son petit doigt, en tendant le bras.
Or, le rapport entre la hauteur de votre ongle et la longueur de votre bras est à peu près le même que celui entre la Lune et la distance Terre-Lune. La longueur d'un bras équivaut à environ cent fois la hauteur de l'ongle, donc la distance Terre-Lune est environ cent fois plus grande que le diamètre de la Lune.
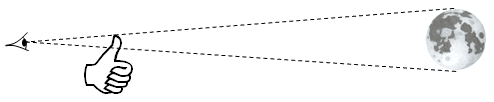
On utilise le fameux théorème de Thalès dont on a déjà parlé tout à l'heure :
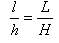
Si l est la distance entre l’œil est le petit doigt h est le diamètre de la Lune L est la distance entre l’œil est la Lune H le diamètre de la Lune Après calcul, on se rend compte qu’on pourrait aligner 30 Terre entre la Terre et la Lune !
Sauras-tu la calculer en stades ?
C'est fantastique, non ?
Mesurer la distance Terre-Lune avec l'ongle d'un petit doigt ! Il fallait le faire ! Oui, je sais : je me répète, mais je suis tout de même fasciné, pas toi ? Quand je pense au premier homme préhistorique qui s'est mis à comtempler le monde qui l'entourait, assis devant l'entrée de sa grotte, je ne peux m'empêcher de penser qu'il est, sans aucun doute possible, passé pour un vrai "boulet" pour ses congénères : non seulement, il faisait fuir le gibier à la chasse tellement il était tête en l'air (c'est le cas de le dire), mais il fallait le nourrir, l'entretenir ! Comme quoi, il y a des boulets indispensables et qui font progresser la communauté !

Avec une distance Terre-Lune dans les roues, je crois que j'ai mérité une bonne retraite, non ?
Distance Terre-Soleil
Et bien, après la conquête de la Lune, les grecs se sont attaqués au Soleil, rien de moins ou plus exactement à son tour de taille et la distance à laquelle il se trouve des dromadaires. Quoi ? L’égocentrisme n’est pas l’apanage des humains que je sache ! C'est encore Aristarque qui a le premier proposé une méthode pour cette mesure. Aristarque soutenait qu'il était possible de mesurer la distance Terre-Soleil en se fondant sur le fait que la Terre, la Lune et le Soleil forment un triangle rectangle quand la Lune est à demi-pleine (premier quart par exemple).
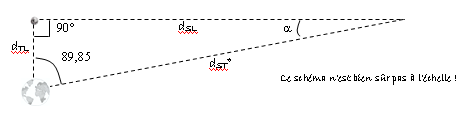
Cela aussi, il fallait y penser ! Malheureusement pour lui, la mesure de l’angle est tellement proche de 90° qu’il n’a pas pu le mesurer avec précision, mais la méthode est là !! Un peu de trigonométrie fait le reste ! La somme des angles dans un triangle est égale à 180° donc il est facile de trouver que l’angle $ \alpha $ au sommet Soleil vaut 0,15°. De plus dans un triangle rectangle, on peut appliquer la trigonométrie élémentaire : On peut alors connaître dST et dSL. On remarquera alors que ces deux valeurs sont vraiment très proches l’une de l’autre. On peut donc mettre environ 400 fois la distance Terre-Lune entre la Terre et le Soleil ! (le Soleil est 400 fois plus loin de la Terre que la Lune) Et les étoiles qui semblent fixes dans le ciel doivent être terriblement loin ! Un peu comme quand on part en vacances : les vaches dans les prés semblent bouger beaucoup quand on passe en voiture, alors que le décor à l'horizon est quasiment immobile !
Ouh là là ! je me sens toute petite !
Tour de taille du Soleil
Et, pendant qu’on y est, pourquoi s’arrêter en si bon chemin ? Il ne reste plus qu’à déterminer le tour de taille du Soleil ! Il serait possible d'utiliser la même méthode que pour la Lune, mais le Soleil est légèrement éblouissant ! Et essayer de le viser et de le masquer avec l’ongle de son petit doigt serait tout de même un peu dangereux pour la rétine ! Mais tout le monde a déjà remarqué que le Soleil et la Lune nous semblent de la même taille, or nous savons bien sûr que ce n'est pas vrai parce que le Soleil nous est beaucoup plus loin que la Lune. Alors, nous attendons une éclipse totale de Soleil, c'est à dire lorsque la Lune passe entre le Soleil et la Terre, les trois étant parfaitement alignés.

La Lune et le Soleil ont tous deux à peu près le même diamètre apparent, il suffit donc d’appliquer une nouvelle fois le théorème de Thalès et le tour est joué ! Comme le Soleil est 400 fois plus loin que la Lune, il a un diamètre 400 fois plus grand aussi ! Et voilà comment Eratosthène, en mesurant le tour de taille de la Terre, donna quasiment une idée de la dimension du système solaire. Les étoiles dans le ciel sont si petites vues d'ici, qu'elles doivent se trouver à des distances beaucoup plus grandes encore, mais là, c'est une autre histoire !
Et aujourd'hui, à Nice ?
Il « suffit » de disposer de miroirs à la surface de la Lune, et de chronométrer la durée d’un aller et retour d’un faisceau laser. Connaissant la vitesse de la lumière, ce n’est ensuite plus qu’un jeu d’enfant ! En juillet 1969, l’Homme a marché sur la Lune pour la première fois et plusieurs miroirs ont été déposés lors de différentes expéditions Apollo. Il y en a entres autres sur les véhicules lunaires Lunokhod 1 et 2. Je dis l'Homme avec un H majuscule pour dire que c'est l'Humanité qui a été capable de le faire (il paraît qu'ils en sont incapables aujourd'hui...). Ils auraient mieux fait d'envoyer des Dromadaires avec un grand D, les mauvaises langues ont dit que nous étions trop lourds. Bien sûr nous savons que toi lecteur, tu n'es pas dupe. Bref, je me serais quand même bien offert une ballade lunaire au clair de Terre...Mais sans ma douce et belle, cela ne valait pas la peine : quand je pense que des hommes sont assez goujats pour cela !
Enfin ! Tu peux distinguer l'emplacement de quelques uns d'entre eux sur la jolie photo centrale. Ces miroirs sont de fabrication française (Aérospatiale de Cannes) et doivent renvoyer la lumière qu’ils reçoivent exactement dans la même direction. Comme bien souvent en physique, le principe de l'expérience est très simple, mais sa réalisation plutôt délicate. Cela demande donc du doigté, en effet :
- Le miroir lunaire est petit : 690 cm² (7 centième de m²). Tu ne t'imaginais tout de même pas qu'il était possible d'embarquer à bord de la fusée, un miroir gigantesque, d'autant plus qu'il ne fallait surtout pas le poser sur le sol. Pourquoi ? Le simple fait de le poser sur le sol (et de marcher autour) aurait soulevé tellement de poussière qu'elle aurait inévitablement recouvert le miroir en retombant. Et un miroir poussièreux est totalement inutile ! Non, il a fallu très précautionneusement, fixer les différents miroirs, qui sur un véhicule lunaire abandonné à son triste sort sur la Lune, qui sur des supports solidement fichés dans le sol. Le miroir doit être à une hauteur minimale de un mètre au dessus du sol.
- Un télescope terrestre envoie un faisceau laser en direction de la Lune en espérant toucher un miroir pour être ensuite retourné à l'envoyeur. Le télescope est équipé d'un récepteur qui détecte le retour du faisceau. Mais, pendant les 2,5 secondes que dure l’aller et retour, le télescope s’est déplacé de quelques 900 m (sous des latitudes de 45°) à cause de la rotation de la Terre sur elle-même. Il est donc difficile de détecter le retour.
- Une horloge capable de mesurer des durées très faibles : de l'ordre de la picoseconde (un millième de milliardième de seconde !). On utilise pour cela une horloge atomique comme celle de l'observatoire de Besançon par exemple.
- De plus un laser très puissant est nécessaire : rends-toi compte : de l'ordre de 100 Gigawatt (cent milliards de watt !) et malgré cela, sur cent milliard de milliard de photons émis, un seul sera reçu à l’issue de l’aller et retour !
- Les tirs sont effectués en escargots dans la zone où est supposé se trouver le miroir, jusqu'à l'obtention d'un signal retour.
- Et bien sûr, il doit faire beau ! Et là, franchement, je trouve qu'il pleut vraiment beaucoup trop à Nice !
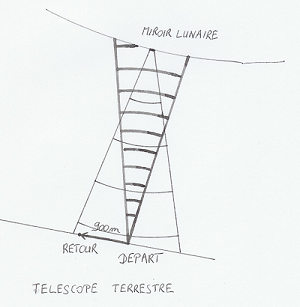
Ah, tu ne savais pas ?
L'Observatoire de la Côte d'Azur (OCA) s'occupe entre autres de télémétrie laser (vers la Lune ou d'autres satellites lancés par les hommes) Ces miroirs sont aussi la preuve que les américains ont bien foulé le sol lunaire, au cas où certains en douteraient !! Et, il semble qu'ils soient nombreux, à voir le nombre de sites internet négationnistes fleurir sur la toile ! Heureusement que tu es là et que tu ne lis pas n'importe quoi ! Donc, le faisceau laser a un diamètre de l’ordre de 1,5 millimètre au départ de la terre. Arrivé sur la lune, le diamètre est de quelques kilomètres (il ne faut pas rater le miroir lunaire !) Sur la lune, la surface éclairée par le laser est donc environ un milliard de fois plus grande que la surface du miroir. Le faisceau est à peu près élargi dans la même proportion lors du retour pour ne pas manquer le télescope. Chaque tir est composé d’une impulsion d’environ 300 ps ($10^{-12}$ seconde). Bilan : le nombre de photons dus au laser reçus par le télescope est d’environ 1 tous les 100 tirs soit environ un photon sur cent milliards de milliards ! Il faut donc réitérer la mesure un grand nombre de fois et moyenner les résultats. La meilleure série obtenue (13 Février 1998) a été de 613 retours sur 10 mn soit sur 6000 tirs. On peut ainsi connaître la distance Terre-Lune au centimètre près !
Petit hommage aux américains !

Mais comment un miroir peut-il renvoyer la lumière dans la même direction que la lumière incidente ? Je sais bien, cher lecteur, que cette incongruité ne t’a pas échappée. Parce qu'en effet, personne n'est sensé ignorer la loi...de la réflexion ! Un miroir réfléchit la lumière, c'est-à-dire qu'il l'a renvoie dans une direction bien particulière : le rayon réfléchi est toujours symétrique au rayon incident par rapport à la normale au miroir. Le rayon réfléchi ne repart donc pas dans la direction du rayon incident sauf s'il est perpendiculaire au miroir, ce qui est plutôt rare.
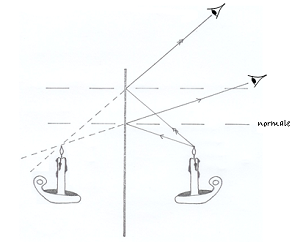
Par construction et en utilisant cette loi, on remarque alors que l'image de l'objet est symétrique à l'objet par rapport au miroir : un droitier qui se brosse les dents devant son miroir voit en fait un gaucher se brosser les dents ! Et en plus, de l'autre côté du miroir ! Comme Alice ! C’est vrai : voilà un phénomène qui m’a toujours frappé et ce depuis que je suis petit dromadaire. Chaque fois que j’allais boire un coup à l’oasis du coin et que j’approchais mon petit museau de la surface de l’eau, voilà qu’un autre petit dromadaire vient boire lui aussi, mais sous l’eau. Inutile de dire que la première fois, j’ai eu une peur bleue. Mais la soif a fini par avoir le dessus. J’ai fini par m’habituer, mais je suis tout de même toujours surpris qu’il ait soif exactement en même temps que moi. Aujourd’hui, je l’ai adopté : c’est en quelque sorte mon frère.
Drôle de miroir !
Avec un miroir double : deux miroirs perpendiculaires l'un par rapport à l'autre :
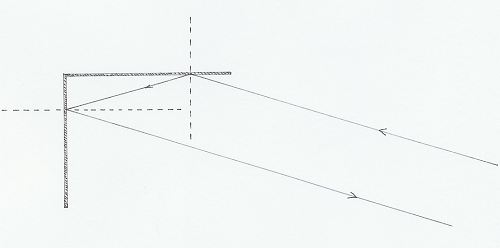
Et hop ! Retour à l'envoyeur Je suis sûr que tout le monde l'a déjà vu, mais sans le voir ! Il existe beaucoup de magasins dont la vitrine a deux miroirs (ou vitres) perpendiculaires. Quand on passe devant, on se voit toujours quelque soit notre position ! Et figure-toi que si tu lèves la main droite (tu n'es pas obligé de dire "je le jure") figure toi que tu te vois lever la main... droite ! C'est le principe du catadioptre qu'on voit sur les pédales ou les roues de ton VTT. A propos de miroir ! Un homme hésite, en se coiffant... Raie à droite ou à gauche ? Le mieux, c'est d'essayer ! Il choisira le côté qui lui plaît le plus... dans le miroir ! C'est-à-dire, qu'avec la raie à gauche, il voit un homme avec la raie à droite et vice-versa. S'il préfère la raie à droite (dans le miroir), par exemple, il se sera en fait coiffé avec la raie à gauche, c'est-à-dire celle qui lui plaît le moins !!! Conclusion, il vaut mieux choisir la raie au milieu.
